Bandwidth and Available Ratios
Since Pythagoras, it's been known that consonance and dissonance relate to frequency ratios.Dissonance increases as the denominator goes up.
Here's a representation of all possible ratios up to some maximum denominator. They represent possible intervals.

Four units of possible ratios
Real-world sounds are not single frequencies. Usually, violins are narrow-band, timpanis are wide-band, and by frequency we mean central frequency. Overlapping bands cover a range of ratios.
Wide-band sounds-- a kindergarten choir, or a crowd singing "Happy Birthday"-- are harmonically less clear. Maybe familiar consonances are ironically replaced with nearby dissonances?
A working assumption accepts the lowest-denominator possibility as the intended one (on the principle: hoofbeats? think horses, not zebras).
Wide-band intervals crowd out nearby dissonances. Purer, narrower sounds have more intervals available.
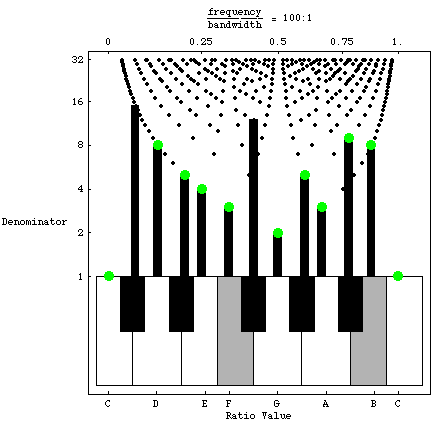
The relationship is illustrated by the Dissonance Forest graph. Moving down the Y-axis, bands widen and hide nearby high-denominator ratios. Moving up the Y-axis, bands narrow and new possible intervals peek through.

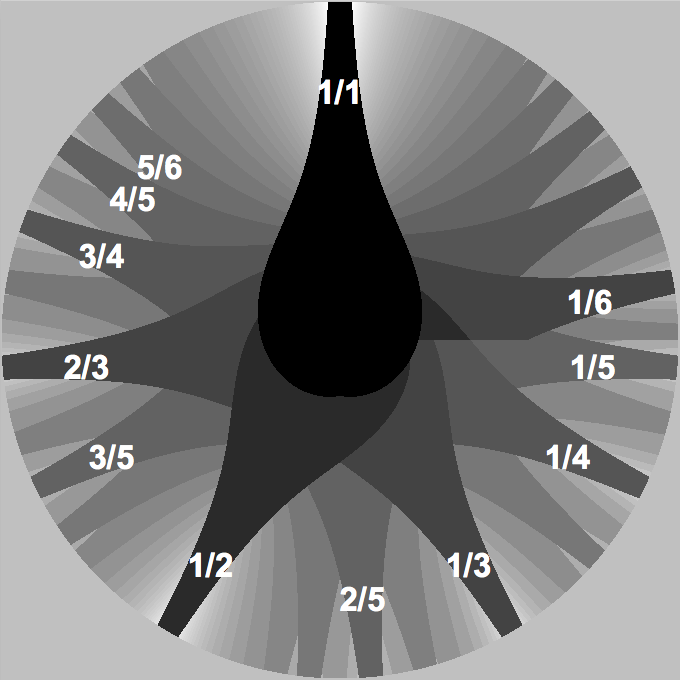
Dissonance Forest: available intervals by bandwidth
Well-tempered Bandwidth
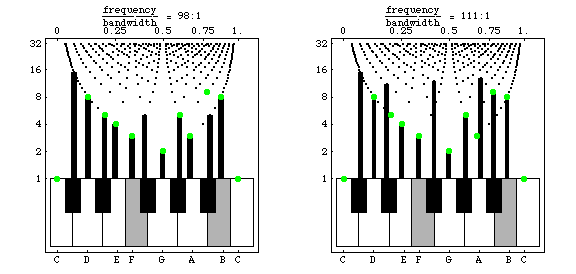
A well-tempered piano tunes notes to be near ideal target ratios.Is there a single bandwidth that evokes the target ratio for all well-tempered frequencies?
Answer: yes, at a frequency-to-bandwidth ratio of about 100:1.
If the bandwidth is a little higher or lower, some intervals fall away from the target:
Dissonance Wheel
Octaves repeat, so the "dissonance forest" can be also pictured wrapped on a circle: